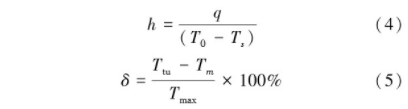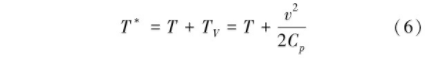分度热电偶时参考端温度对测量结果的影响
发布时间:2022-10-08
浏览次数:
摘要:为分析涂层测温结构对航空发动机涡轮导向叶片表面温度测量精度的影响,建立了测温结构的数学模型。以热流耦合理论为基础,采用SST-γ-θ湍流模型求解动量和能量方程,研究了涂层位置、涂层厚度和前缘形状对叶片待测区城温度的影响。研究表明:考虑转捩的SST-γ-θ具有较好的数值计算精度,其温度计算结果与试验误差不超过10%;当涂层前缘位于转捩点附近时,涂层对测量精度的影响较大;与叶盆中部和叶背前缘相比,涂层对叶背中部和叶背尾缘的测温精度影响较小;当涂层厚度小于总温边界层厚度时,测量精度几乎不受影响;将涂层前缘加工成圓角可以有效减小涂层对叶盆面测温精度的影响。
航空发动机作为航空飞行器的动力装置,正不断向大推力、大推重比的方向发展。随着航空发动机性能的提高,其工作温度也相应地持续提高。20世纪60年代以来镍基单晶合金材料的耐高温性在涡轮叶片制造中提高了102℃。近年来,发动机工作温度接近甚至超过材料的许用温度,热端部件表面温度的准确测量对发动机设计水平的提高具有重要的现实意义。
目前,涡轮导向叶片表面温度主要的测量方法有传统
热电偶测温、红外辐射测温[3]、示温漆测温、
薄膜热电偶测温等。由于热电偶具有结构简单.制造方便、测量范围广、精度高、惯性小和输出信号便于传输等诸多优点,一直都是航空发动机叶片测温的主要测量元件。通过热电偶测量叶片表面温度的主要难点在于安装和制备方法。由于叶片表面光滑,传统使用中热电偶是通过填埋或金属蒙皮的方法固定在金属表面的。采用填埋安装时,由于叶片厚度方向的温度梯度,测量点温度难以与表面保持一致,因而无法准确测量叶片表面温度,此外还会造成试件表面的破损。而采用金属蒙皮焊接固定又会导致热电偶受感部周围存在缝隙,造成较大的接触热阻。为解决传统热电偶安装方法中存在的弊端,提高涡轮叶片表面温度测量的精度,一种将熔融态耐高温绝缘材料Al2O3粉末直接喷涂至涡轮叶片基底上的热电偶安装方案,简称为涂层测温。该方案的工艺流程为:①表面吹沙处理,增加待测表面粗糙度;②使用高能等离子喷枪喷涂Al2O3粉末,材料,形成绝缘层;③利用高温胶带和等离子材料喷涂工艺完成功能层制备;④利用高温胶带和Al2O3粉末制备保护层;⑤通过平行微隙焊接工艺和激光焊接技术完成热电偶裸丝与后端高温补偿导线连接,最后将高温胶带揭去,完成涂层制作。
相对于金属蒙皮Al203涂层、金属基底和热电偶头部之间几乎不存在接触间隙,是一种新式的热电偶安装制备工艺。但涂层具有一定的厚度,其边缘易对涡轮叶片表面的燃气流动产生干扰,该测量方法的准确性还有待进一步的评估和验证。
由于实际涡轮叶片测温试验中,影响涂层测温精度的因素较多,如固体导热接触热阻、辐射环境、信号传输及处理等,难以通过试验手段精确分析某单一因素对误差的影响,且多次试验成本较高。近年来,随着CFD热流耦合技术的发展,对流体换热问题的计算精度有较大提高,较多研究者开始采用仿真方法预测涡轮叶片的工作环境和表面温度。
为详细分析涂层测温中涂层对叶片表面温度和燃气环境的影响,以MarkI叶片为原型,根据实际情况,建立4个典型位置的涂层模型,基于热流耦合仿真技术,讨论涂层的位置、厚度和前缘形状对涡轮导向叶片表面温度的影响,为提高叶片表面温度测:量准确性,修正热电偶测量误差提供参考。
1物理模型及计算方法
1.1计算模型
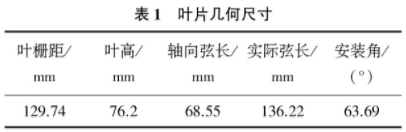
所研究的叶片叶型数据参考文献[16]的叶片平面坐标和高度数据,通过Workbench-DM建模软件中的样条线(curve)拟合而成,然后经放样计算获得整个叶片的三维模型。该叶片为MarkII型导向叶片,其几何参数如表1所示。
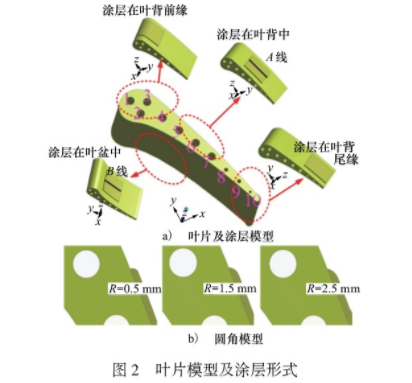
典型的热电偶涂层安装试件如图1所示。根据.热电偶涂层的结构,在MarkI叶片模型上,建立了4个涂层的典型位置,分别位于叶背前缘、叶背中、叶背后缘、叶盆处,标准的涂层尺寸为50mmx50mmx1mm。叶片模型及涂层的位置如图2所示。其中,图2a)中2处黑线位于涂层下方叶片表面50%叶高处,表示实际使用中热电偶测量点可能处于的位置,命名为A线和B线。考虑到涂层多采用喷涂形式,边缘一般会带有一定的圆角,为研究圆角半径R对测量点附近温度的影响,在1mm厚度涂层模型的基础上建立了3种圆角形式,如图2b)所示。

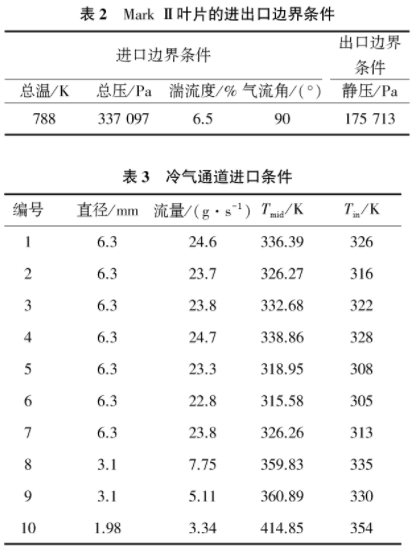
选用5411号试验工况,其进出口边界条件如表2所示。叶片中有10个径向圆柱形对流冷却孔,其直径,冷却气体质量流量、中径处平均总温Tmid和冷却气体进口总温Tin见表3,冷却气体出口静压为175713Pa。
1.2材料参数
数值计算中,流体的工质设为理想可压燃气,其定压比热容Cp为1004.4J/kg·K,分子黏性μ和导热系数K均表示为温度T的函数

涂层的材料为氧化铝(纯度为96%),其密度为3800kg/m³,导热系数为25W/m·K,比热容为880J/kg.K。
1.3网格划分
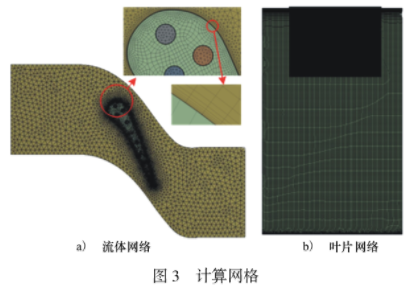
对湍流的模拟选用Menter和Langtry提出的间歇因子与动量厚度的雷诺数双方程SST-γ-θ湍流模型[2]。该转捩模型是基于局部变量的转捩模型,并对前人提出的模型作了较大改进,通用性和准确性都得到很大提高[23]。网格采用ANSYS-Workbench提供的Mesh工具进行划分。由于边界层内流体的速度和温度变化较大,需要对边界层内网格进行加密。根据进出口条件估算叶片附近气体的雷诺数为10量级,为满足SST-γ-θ模型计算精度要求,需要y*数尽可能接近于1。根据CFD-Online提供的y'计算器的估算结果[24],将近壁面第一层网格厚度划分为1μm,此后每层间距以1.5的比率增加,共划分了15层近璧面网格。在叶片冷却通道内以同样方法生成近壁面网格,其第一层网格厚度为0.01mm,增长比为1.5,共15层。燃气区采用混合网格划分,叶片和涂层部分则采用以六面体为主导的网格划分。涂层部分在涂层厚度方向上划分为10层网格,在流-固、固-固交界面网格进行加密。网格交界面数据采用generalgridinterface(GGI)格式传递。经网格独立性试验选择网格总数约为908万。其中,流体网格为775万、叶片网格为70万、涂层网格为64万,网格如图3所示。
1.4求解过程
边界设置为无滑移壁面,燃气两侧采用周期性边界条件。传热模型为总能模型,求解格式为二阶向后欧拉法,湍流数值采用精度高求解格式。当气体马赫数达到0.3以上时,气体动能对换热的影响变得显著,因此设定传热模型为总能模型,并使用CFX特有的高速壁面换热模型增加求解精度。当连续性、动量、湍流和能量各残差曲线和设定的监测点温度趋于稳定,所有的流体进出口质量流量相对误差小于10
-6时,认为计算收敛。为方便对比定义对流换热系数h、相对温差δ为
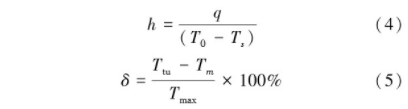
式中,T0为燃气入口总温,Ts表示固体温度,Ttu为tu带有涂层时的叶片温度Tm为无涂层叶片表面温度,max为无涂层叶片最大温度,根据仿真结果,其值取为688K。
2结果及讨论
2.1计算结果验证
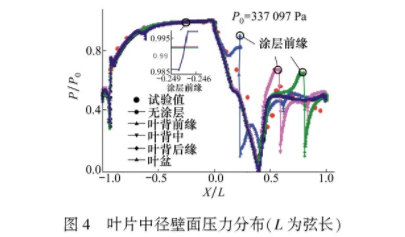
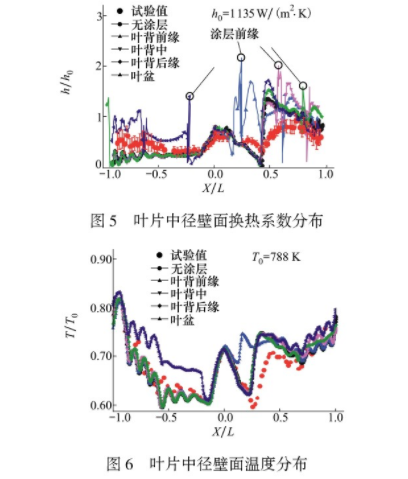
数值策略的验证采用了Hylton[17]报告中5411号试验的结果数据。分别取无涂层及涂层厚度为1mm时,50%叶高处的压力、对流换热系数及温度结果与试验值对比,对比结果如图4至6所示。由图4可见,无涂层叶片压力计算结果和实验数据吻合较好,在吸力面上轴向弦长(轴向弦长记为L)约X/L=0.2和X/L=0.4处前后都存在较大的压力梯度。值得注意的是此处SST-γ-θ模型的预测结果与实验值有一定的偏差,这是因为激波发生附近边界层分离诱发转捩,边界层内梯度较大,产生所谓“激波-边界层”相互作用。在燃气流经激波面时,燃气中的压强、密度、温度和流速都会发生较大的变化,因此激波点可视为间断点,具有很强的非线性特征,造成较大的计算误差,这也是目前一个公认的有待解决的数值计算问题。
如图6所示,激波附近叶片表面温度突然下降后急剧上升,原因是转捩点附近发生附面层分离,气体内能向动能转化,燃气温度下降。激波后附面层重新生成,气体的湍流动能得到加强,换热速度增加,温度上升。由图5和图6可知,无涂层叶片表面中径处传热系数h和无量纲的静温T的分布趋势与实验相仿,尽管在吸力面有一定偏差,但多数偏差点小于10%,在可接受范围内。
2.2涂层位置的影响
涂层在叶片不同位置时的表面流线分布及表面温度分布如图7所示。如图7a)所示,叶片表面的流线在涂层周围形成绕流,在涂层前后缘形成漩涡。当叶片表面覆盖涂层时,表面流动状态与流体流动时遭遇障碍物的情况相似。根据张俊婷等人[28]的研究,当流体流经长方体障碍物时,在障碍物的最高点处即出现边界层分离,且长方体的回流区比半圆形障碍物和流线型障碍物大。由于涂层的结构近似为长方体,故在涂层的前壁面最高点处也会发生边界层分离现象,分离点的气体流速及换热系数波动较大。如图4和图5所示,涂层前缘和尾缘均出现较大的压力和传热系数波动。尽管局部的传热系数较大,但相对于整个涂层边缘处的面积很小,经过涂层的展向传热(固体导热)边缘处的温度分布仍比较均匀。如图7b)所示,涂层边缘处温度略微升高,可以推断实际使用中测量点靠近涂层边缘时,可能导致测量值偏大。
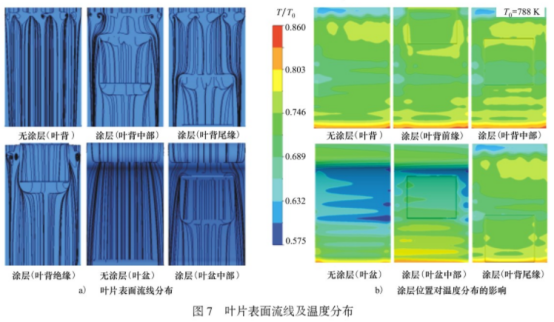
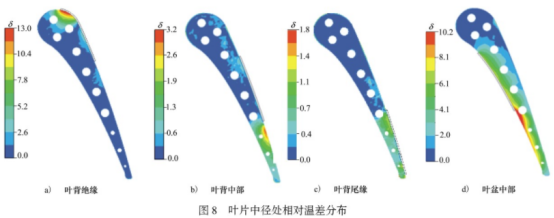
图8为涂层位于不同位置时,叶片中径面的相对温差分布。由图中可知,涂层处叶片温度明显升.高,当涂层位于叶背前缘时,温度波动最大,相对温差达到12.8%。根据图4至图6的计算结果,涂层.前缘位于转捩点附近时,易发生速度边界层分离造成较大的温度波动。使用涂层测温时应避免涂层前缘位于转捩点附近。同时,可以观察到涂层的前缘和尾缘处,叶片温度明显高于其他位置。
2.3涂层厚度的影响
引入涂层后,叶片表面的燃气环境所受影响较大,如图4和图5所示,涂层前后均出现明显的波动,除此之外涂层还导致转捩、回流等现象发生。由于涂层周围气体流动的状态非常复杂,因而单独讨论其对速度边界层或热边界层(即:温度边界层)的影响都不足以说明引人涂层后叶片温度发生改变的原因。叶片与燃气间热交换过程的本质是气体内部分子碰撞金属表面将动能传递给金属表面分子的过程。在不考虑辐射情况下,气体和固体间的热交换的驱动力由两部分组成,一种为大量气体分子的宏观运动,即动温,Tv;一种为气体分子的无规则运动,即静温,两者之和为气体的总温,其表达式为
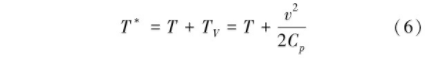
式中,υ为气体的流速。为分析涂层对叶片对流换热的影响,定义总温边界层的厚度为从物面到约等于99%外部流体总温处的垂直距离。取涂层前缘周围6mmx8mm的局部区域为分析对象,其近壁面气体总温的分布形式如图9所示。
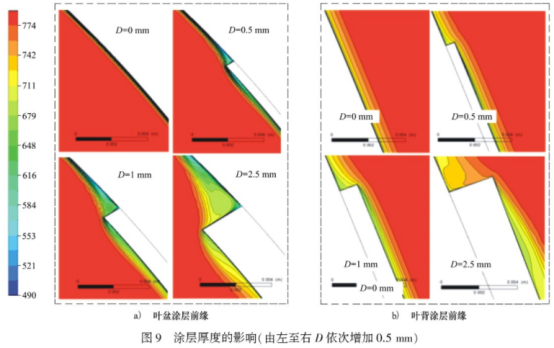
总温边界层的厚度用于表示单位面积内固体能够从气体内获得能量的大小。工程上希望采用涂层测温方法后,总温边界层厚度可以尽量维持原状,以确保叶片温度不受到涂层的影响。因此,在理想情况下涂层厚度应尽可能小于总温边界层的厚度。由图9可知,叶盆面总温边界层的厚度低于叶背面,因此,叶盆面的总温边界层对涂层的厚度更加敏感。对比叶盆区和叶背区涂层对总温边界层的影响可知,在同样厚度下,叶盆区的总温边界层厚度低于叶背区。进一步对比总温边界层厚度的相对增加量(总温边界层厚度的相对增加量=(添加涂层后的总温边界层厚度-无涂层时的总温边界层厚度)/无涂层时的总温边界层厚度))可知,叶盆区总温边界层厚度的相对增加量明显大于叶背区。这也是叶背区涂层对测温的影响远小于叶盆区的主要原因。
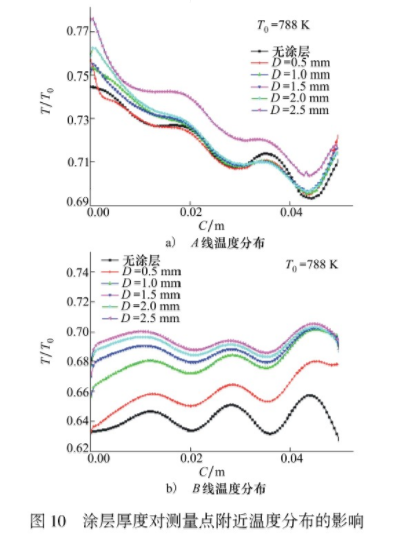
图10为涂层厚度对标记线A、B无量纲温度的影响,定义C为涂层沿流线方向的长度。如图10a)所示,叶背处涂层厚度对温度的影响小于叶盆面,当涂层厚度大于0.5mm时,涂层厚度对叶盆区温度的影响增加;当涂层厚度大于2mm时,叶背面的温度才开始受到较大的影响,这进一步说明了总温附面层厚度与涂层厚度之间的关系。从计算结果分析,仅当涂层厚度小于0.5mm时,热电偶涂层才不会对涂层测温的精度造成较大的影响。此时,有涂层时的温度与无涂层时温度接近相等,平均相对温差仅为2%。
2.4涂层圆角的影响
图11为涂层前缘平面垂直于叶片表面和涂层前缘为圆角时的马赫数分布图。当涂层前缘平面与叶片表面垂直时,涂层前缘的平面阻碍了流体的运动。气体直接撞击涂层的前缘,形成了很小的气旋(如图11中速度矢量图所示),气旋消耗了气体的动能并降低了气体的流速,因而流过垂直涂层壁面的气流没能加速形成激波。当涂层前缘为圆角时,流线型的涂层前缘减小了气动阻力。在这种情况下气体的流速进一步增加,在流经涂层前缘后形成了一个弱激波。与叶背前缘的强激波相似,燃气流经涂层前缘的弱激波后,燃气的温度先下降后升高。
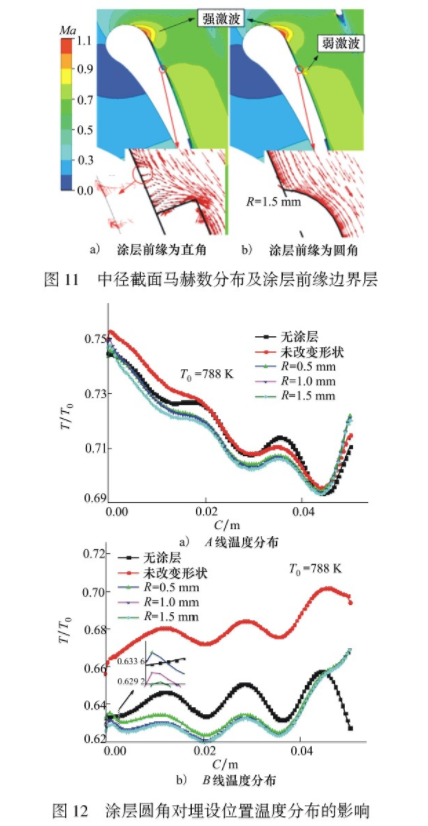
图12为涂层前端圆角的半径对标记线A、B无量纲温度的影响。
如图12a)所示,当位于叶背中部的涂层前端为圆角时,受到激波的影响,沿燃气流动方向涂层区的温度先偏小再增大。如图12b)所示当位于叶盆区中部的涂层前缘为圆角时,沿燃气流动方向的温度.同样呈现先偏小再偏大的规律,但两者的作用机理是不同的。当叶盆区的涂层前缘为圆角(流线型)时,涂层前端不会发生激波。此时,涂层对叶盆区测温的影响仅体现为涂层自身的隔热作用。由于叶盆面的对流换热速度较低,涂层起到了明显的隔热作用。
3结论
基于热流耦合技术研究热电偶安装涂层对涡轮导向叶片温度测量精度的影响,分别比较涂层厚度、位置及形状对常规测量点附近气动参数及温度的影响,主要结论如下:
1)叶片表面不同位置的温度受涂层的影响程度不同,叶背区中部和尾缘的涂层对测温的影响远小于叶盆区中部和叶背区前缘的涂层,当涂层前缘靠近叶片转捩区时,测温误差将大幅增加;
2)热电偶涂层会使总温边界层的厚度增加,相比于叶背,叶盆面的总温边界层厚度受涂层影响较大,当涂层厚度等于或大于总温附面层时测量误差将大幅度.上升,当涂层厚度小于0.5mm时,涂层测温的精度达到98%;
3)涂层前缘为圆角时可有效避免涂层前缘的燃气流发生流动滞止,从而提高涂层测温的精度,与叶背中部相比,涂层前缘形状对叶盆中部的测温精度影响更大。