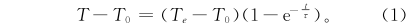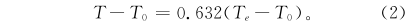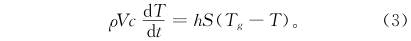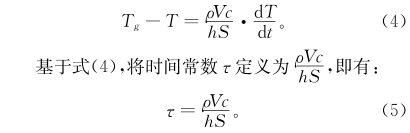高温火焰法在热电偶动态特性分析

摘要:为研究热电偶温度传感器在静态爆破试验中的响应特性,采用高温火焰法测得K型热电偶的时间常数为851.660ms;在热电偶不满足测试要求时,通过系统逆建模的方法建立了热电偶的动态补偿滤波器模型;加上动态补偿滤波器将热电偶温度传感器在瞬态高温火焰温度场中的时间常数补偿为93.583ms,达到了补偿的目的。对补偿前后热电偶的幅频特性进行分析,结果表明，补偿后热电偶测温系统的频带明显拓宽。
　　进行爆温测试时,瞬态高温测试所得测试结果的准确性与传感器的响应特性息息相关甲。在应用广泛的接触式测温中,热电偶时间常数的大小反映其动态特性的优劣问。常见的用于时间常数测试的经典方法有水浴测试法、热风洞测试法和瞬时电加热测试法。热电偶温度传感器的响应特性因其所处测温环境的不同而差别极大6,若仍采用常规的测试方法,由于温度场不同,所得时间常数就不能真实反映传感器在静爆场中的响应特性。
　　采用高温火焰法,在实验室现有技术条件下研究传感器的动态响应特性的，并以此为基础,针对目前热电偶的动态响应特性无法满足爆温测试需求的问题[8],设计了热电偶的动态补偿滤波器模型，以改善其在高温火焰场中的响应特性。
1热电偶的时间常数
　　热电偶的阶跃响应表达式为
 
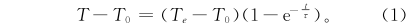
　　式中:T为指示温度;T0为初始温度;Te为最终的阶跃温度值;t为时间;τ为时间常数。
　　式(1)中,当t=τ时,可得:
 
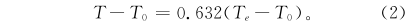
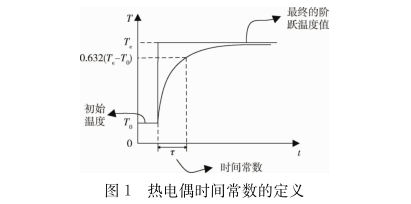
　　由式(2)可知，时间常数就是T与T0之差达到温度阶跃值(Te-T0)的63.2%时所对应的时刻与初始温度T0所对应时刻的时间差,时间常数的定义，如图1所示。
 
　　在实验研究或工程应用中,对热电偶进行分析时，都是在忽略热传导、热辐射及其内部温度分布的理想条件下进行的,其能量方程为
 
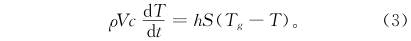
　　式中:ρ、c分别为组成热电偶金属的密度、比热容;V为热电偶热端热结点的体积;T为热电偶测量端的瞬时温度值;h为导热系数，可因热电偶测温环境的不同而不同;S为热节点表面流体薄膜的面积;Tg为被测气流的真实温度。ρ、c、V、S均为传感器的物理参数,与测温环境无关。由式(3)可得:
 
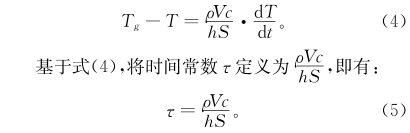
　　式(5)表明,时间常数不仅与其物理参数有关，还与其所在温度场环境有关。
2火焰场中热电偶的时间常数
　　采用一种高温火焰法探究温度传感器在高温火焰场中的动态特性。
　　一直以来,在接触式的爆温测试中,应用最为广泛的是标准的K型热电偶和非标准的钨铼合金热电偶([0。目前,虽然一些新研制出来的钨铼合金热电偶在响应速度和测温范围方面优势明显,但不宜在空气或含氧环境中使用。选用K型细裸线热电偶进行研究,所选热电偶的基本指标参数见表1。
 
2.1高温火焰法
　　为了得到与热电偶在爆温测试中表现最为接近的传感器的动态响应特性,所采用的高温火焰法的具体工作流程如图2所示。
 
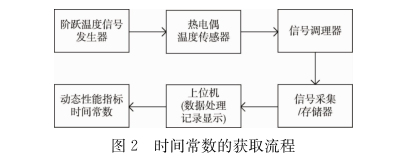
　　图2中，温度阶跃信号发生器是高温火焰法最具特色的部分,由纵向直线导轨、竖向大挡板、快速吸附片、带竖向小挡板和滑轮滑块、快速弹射装置(图中未画出)、高温火焰温度源及隔热箱组成。高温火焰测试法测试系统的结构如图3所示。
 
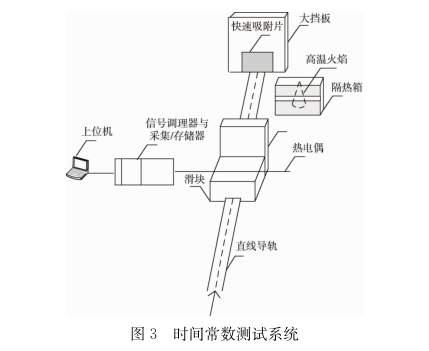
　　图3中,与火焰温度源法[11的不同之处在于,在高温火焰温度源_上加了隔热箱,并在隔热箱上留有1个与热电偶在同一水平线上的用于热电偶自由出人的开口。这样改进后，不仅可以使高温火焰温度源免受外界因素的扰动，而且还可以有效避免高温火焰温度源在时间常数测试过程中的热量散失,从而保证用于产生阶跃温度信号的高温火焰温度源的稳定性,使高温火焰法更具有实用价值。
2.2时间常数的测试
　　采用高温火焰法的实验步骤如下:
1)备好纵向直线导轨,并将其固定在实验台上，然后备好载有热电偶的滑块。
2)调整高温火焰温度源的位置,使被测传感器快速滑动与大挡板吸合的时刻偶结能完全置于火焰中。
3)按照图3所示连接时间常数测试系统。
4)确认各部分之间的连接方式无误后,对测试系统通电,并在计算机界面进行相关参数的设置。
5)打开高温火焰发生器的开关,启动弹射仪,使被研究热电偶以很快的速度滑动，当偶结完全置于火焰中时,热电偶便可受到温度阶跃信号的激励。
6)在上位机界面读取实验结果。
　　由实验结果读取被测热电偶的时间常数,热电偶的温度阶跃响应如图4所示。
 
　　图4中,游标1指示的是温度阶跃信号发生时，热电偶初始温度为0的时刻，即1867.536ms;游标0指示的采集到的温度值1348.558℃与初始温度值的差值达到采集到的稳态值的63.2%,即852.289℃,所对应的时刻为2719.196ms,则此时被测热电偶的时间常数是851.660ms。
　　由时间常数分析式(4)和式(5)可得:
 
　　由式(9)可知，当热电偶输人为阶跃信号时,其动态响应误差会随着时间的增大而减小。且当t>3τ时,热电偶的测量值基本接近真实值。可认为当热电偶的响应随时间不再有变化时,所测温度与环境温度之和即为火焰的真实温度。
2.3验证实验
　　为了验证高温火焰法中温度阶跃信号发生器的有效性,构建了1个阶跃信号,输人给1个τ为851.660ms的一阶响应系统,将其阶跃响应与时间常数为851.660ms的实际的阶跃信号进行比较,结果如图5所示。
 
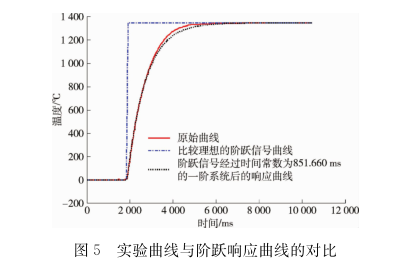
　　图5显示,将1个阶跃信号输入给τ为851.660ms的一阶响应系统,其响应曲线与高温火焰法中热电偶温度传感器的响应曲线非常接近。因此，该高温火焰时间常数测试法产生的激励是1个比较理想的温度阶跃信号。
3热电偶动态特性补偿数
　　由于被研究热电偶在瞬态高温火焰温度场中的时间常数高达851.660ms,-方面,这样的响应速度显然无法满足爆温测试的要求;另一方面,也很难通过优化细裸线热电偶的物理参数来提高其动态特性，因此,需采取其他合适的方法来对热电偶的响应特性进行改善。
3.1逆建模法
　　所谓系统逆建模法，就是直接利用被研究热电偶温度传感器时间常数测试时的输人、输出信号来建立传感器逆模型的一种新型建模方法[13],其基本原理如图6所示。
 
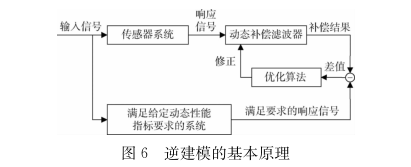
3.2热电偶响应特性的补偿
　　《中华人民共和国国家计量技术规范》中明确指出,给传感器加温度阶跃量时,产生阶跃平台所用的时间须不大于被研究测温器件时间常数的10%14]。传感器的时间常数为851.660ms,因此，建立热电偶的补偿模型时,可构建1个，上升时间80ms的斜坡信号作为传感器补偿模型的输出量;另外,可将所得的热电偶的温度阶跃响应作为补偿器模型的输人量。
在众多常用的优化算法中,由于粒子群优化算法(PSO)独具特色,不仅算法简单、收敛性好,而且搜索速度快、全局搜索能力也强，所以，应用甚广。
3.2.1粒子群优化算法(PSO).
　　采用PSO寻找最佳解时,将潜在的解视为D维空间中的1个点，即粒子(Particle)。建立补偿器模型的过程中，首先设模型的系数矩阵为PSO算法中的粒子;然后设D维空间中的粒子数为m。粒子的特点如下。
3.2.1粒子群优化算法(PSO)
　　采用PSO寻找最佳解时,将潜在的解视为D维空间中的1个点,即粒子(Particle)。建立补偿器模型的过程中,首先设模型的系数矩阵为PSO算法中的粒子;然后设D维空间中的粒子数为m。粒子的特点如下。
 
3)每个粒子都有1个个体适应度值,粒子间正是通过比较该值来更新自身的最佳位置。
4)所有的粒子组成了1个种群,叫粒子群。粒子群有1个群体的适应度值,同理,粒子会将自己上次所得的适应度值与其当前位置的适应度值相比较,若群体的当前值更优，将其对应的位置作为种群当前的最佳位置,即Pg。
　　令Pg=(pg1+pg2,.,pgD)。PSO的整个优化流程如图7所示。
 
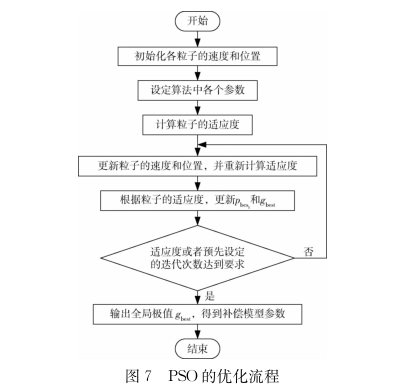
3.2.2热电偶动态补偿模型的建立
　　将采用高温火焰法所得温度阶跃响应和设定的斜坡信号分别作为补偿模型的输入量和输出量,设定粒子数和搜索空间的维数后,随机地初始化每个粒子的速度和位置,便可按照图7的规律在MAT-LAB中实现PSO。寻优完成后,基于PSO的动态特性补偿结果如图8所示。
 
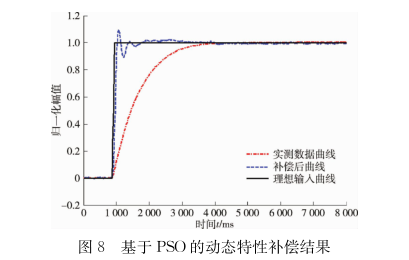
　　图8显示,经过补偿后,被研究热电偶的动态响应特性的时间常数值减小了很多,为93.583ms,响应速度得到了大幅度提升。
3.2.3热电偶测温系统的幅频特性分析
　　在被研究温度传感器的时域指标得到大幅度地提升的基础，上,对时间常数为851.660ms的原始一阶系统的幅频特性、所建立的动态补偿模型的幅频特性及两者串联后的整体幅频特性分别在MAT-LAB环境中进行分析，补偿前后的幅频特性曲线如图9所示。
 
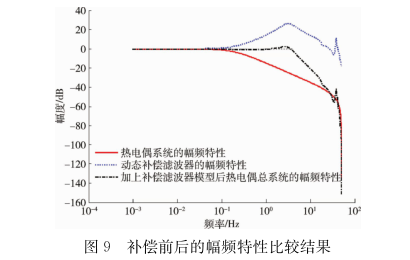
　　图9显示,加上动态补偿模型后,通过滤波器后的频率衰减情况为在接近零轴中间隆起时的曲线对应的频率增大，测温系统的频带得到了很大程度的拓宽。
4结语
　　采用高温火焰法得到了被研究细裸线热电偶的时间常数,并以此为基础,建立了传感器的补偿模型,拓宽了测温系统的频带,有效地改善了其在瞬态高温火焰场中的响应特性,基本满足了爆温测试的需求，所提出的高温火焰法对评估爆温测试中热电偶的真实动态响应特性有一定的实用价值。